本投稿ではPythonを使用して相関係数を求める方法を紹介します。
相関係数は2つのデータに相関関係があるのかを「-1≦0≦1」で示したものとなります。
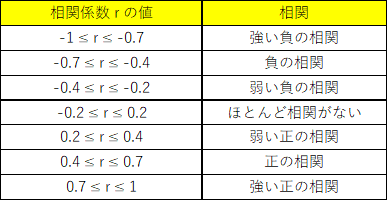
注意しないといけないのは、AとBの相関係数が0.3でBとCの相関係数が0.5だった時にBとCのほうがAとBより相関があると結論付けることはできません。
あくまで相関係数は対象とした2つの確率変数に線形な関係があるのかを示す指標です。
相関係数の求め方
相関係数は以下の通り求めることができます。

この公式は以下の6STEPに分けることができるそうです。
STEP1:2つの確率変数の平均を求める。
↓
STEP2:偏差(各データ値 – 平均)を求める。
↓
STEP3:分散(偏差の2乗の平均)を求める。
↓
STEP4:標準偏差(分散の正の平方根)を求める。
↓
STEP5:共分散(偏差の積の平均値)を求める。
↓
STEP6:相関係数を求める。
本投稿ではPythonで以下の方法で相関係数を求めてみます。
・上記6STEPに分けて相関係数を求める
・numpyモジュールのnumpy.corrcoef関数を使用して相関係数を求める
Python:6STEPで相関係数を求めよう
今回はこちらのデータを使用して相関係数を求めてみます。
english = [50, 60, 70, 80, 90]
math = [40, 70, 90, 60, 100]
-確率変数の平均を求めます。
english_avg = sum(english) / len(english)
math_avg = sum(math) / len(math)
英語の平均点は 70.0 点です
数学の平均点は 72.0 点です
-偏差を求めます。
english_dev = []
for e in english:
e_dev = e – english_avg
english_dev.append(e_dev)
print(“英語の偏差=”,english_dev)
math_dev = []
for m in math:
m_dev = m – math_avg
math_dev.append(m_dev)
print(“数学の偏差=”,math_dev)
それぞれの結果は以下です。
英語の偏差= [-20.0, -10.0, 0.0, 10.0, 20.0]
数学の偏差= [-32.0, -2.0, 18.0, -12.0, 28.0]
-分散を求めます。
english_d = []
for e in english_dev:
e_dis = e ** 2
english_d.append(e_dis)
english_dis = sum(english_d) / len(english_d)
math_d = []
for m in math_dev:
m_dis = m ** 2
math_d.append(m_dis)
math_dis = sum(math_d) / len(math_d)
それぞれの結果は以下です。
英語の分散= 200.0
数学の分散= 456.0
-標準偏差を求めます。
import numpy as np
english_std = np.std(english_dev)
math_std = np.std(math_dev)
それぞれの結果は以下です。
英語の標準偏差は 14.142135623730951
数学の標準偏差は 21.354156504062622
-共分散を求めます。
cov_mul = [e * m for (e, m) in zip(english_dev, math_dev)]
cov = sum(cov_mul) / len(cov_mul)
結果は以下です。
共分散= 220.0
-相関係数を求めます。
cor = cov / (english_std * math_std)
2つのデータ(英語と数学の点数)の相関係数= 0.728492796385774
相関係数を6STEPに分けて求めてみました。
次はnumpy.corrcoefで求めた相関係数の値が同じとなるのか確認してみましょう。
numpy.corrcoefで求める相関係数
上記の方法で相関係数を6Stepに分けて求めましたがNumpyモジュールには
「numpy.corrcoef」という相関係数を求めるための関数が用意されています。
numpyがインストールされていない場合はnumpyをインストールしてください。
> pip install numpy

-numpy.corrcoefを使用して相関係数を求めます。
english = [50, 60, 70, 80, 90]
math = [40, 70, 90, 60, 100]
import numpy
cor = numpy.corrcoef(english, math)
print(cor[0,1])
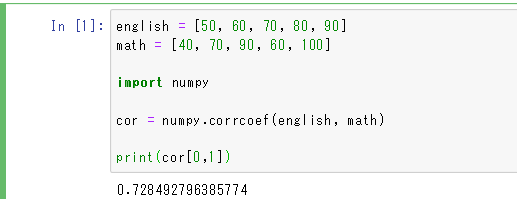
先ほどと同じ値の相関係数を求めることができました。
今回はPythonで相関係数の求め方を紹介しました。
統計については現在学んでいる最中ですのでこれを皮切りにもっと深い知識を習得したいです。
現在は以下書籍で数学に対する抵抗感をなくしたいため学習を進めています。
本書籍は以下の内容を目的としています。
・人工知能に関する専門書を読むために必要な数学基礎力を身につける。
・いくつかの人工知能のアルゴリズムを理解し、数式の意味を理解できるようになる。
今回ご紹介した相関係数に関する情報も載っています。
社会人となって数学から離れていましたが基礎的なところ(中学~高校レベル)から学ぶことができるため良いリハビリとなっています。
ご興味のある方は是非手に取ってみてください。
最後に、Jupyter-Notebookにて6STEPで相関係数を求めた際のエビデンスを載せておきます。
#englishとmathという二つのデータを用意する。
english = [50, 60, 70, 80, 90]
math = [40, 70, 90, 60, 100]
#相関係数を求めるためにはまずはそれぞれの平均を求める。
english_avg = sum(english) / len(english)
math_avg = sum(math) / len(math)
print("英語の平均点は",english_avg,"点です")
print("数学の平均点は",math_avg,"点です")
#偏差(数値 - 平均値)を求める。
english_dev = []
for e in english:
e_dev = e - english_avg
english_dev.append(e_dev)
print("英語の偏差=",english_dev)
math_dev = []
for m in math:
m_dev = m - math_avg
math_dev.append(m_dev)
print("数学の偏差=",math_dev)
#分散(偏差の2乗の平均)を求める。
english_d = []
for e in english_dev:
e_dis = e ** 2
english_d.append(e_dis)
english_dis = sum(english_d) / len(english_d)
print("英語の分散=",english_dis)
math_d = []
for m in math_dev:
m_dis = m ** 2
math_d.append(m_dis)
math_dis = sum(math_d) / len(math_d)
print("数学の分散=",math_dis)
#標準偏差(分散の正の平方根)を求める。
import numpy as np
english_std = np.std(english_dev)
print("英語の標準偏差は",english_std)
math_std = np.std(math_dev)
print("数学の標準偏差は",math_std)
#共分散(偏差の積の平均値)を求める。
cov_mul = [e * m for (e, m) in zip(english_dev, math_dev)]
print("英語と数学の点数の積=",cov_mul)
cov = sum(cov_mul) / len(cov_mul)
print("共分散=",cov)
#相関係数(共分散を2種類のデータから求めた標準偏差で割る)を求める。
cor = cov / (english_std * math_std)
print("2つのデータ(英語と数学の点数)の相関係数=", cor)




コメント